Mastering Breadth First Search in Python (with Working Code)

Breadth First Search (BFS) is a basic algorithm in the field of computer science and graph theory. In comparison to depth-based methods, the BFS traverses nodes layer by layer beginning with a particular source node.  It traverses all the neighbors of a current node in a particular layer and the goes to the next layer. This algorithmic choice has led to BFS being most suitable with discovering the shortest path in unweighted edges and resolving many real-world scenarios including:

• Navigating mazes or grids.
• Performing web crawling.
• Analyzing connections in social networks.
• Finding the minimum number of moves in puzzle-based problems.

 

How BFS Works

The fundamental concept of BFS is to manipulate nodes with a queue data structure. This is what happens in stages:

• Start at the source node: Mark it as visited and add it to the queue.
• Process the queue: Remove a node off the front, and explore all its unvisited neighbors and add its neighbors to the queue.
• Repeat the process: Process the nodes while going level by level in the graph till you reach the empty queue.
• Track visited nodes: To make it efficient, put a set or a boolean array to avoid walking through the same node.

The primary benefit to BFS is that the algorithm will always give the minimum path based on edges in the unweighted graph. On the contrary, Depth First Search (DFS) may become trapped down a particular route without looking elsewhere.

 

Key Applications of BFS

BFS has wide-ranging uses in algorithmic problem-solving:

• Shortest Path Problems: BFS is the preferred method for determining the minimum steps or moves in unweighted scenarios, such as grid-based puzzles.
• Tree Level Traversals: BFS is also known as level-order traversal when applied to trees.
• Web Crawling: Search engines use BFS-like methods to crawl and index web pages layer by layer.
• Networking & Social Graphs: BFS helps analyze reachability or find the shortest connection path between two nodes in a network.
• AI & Game Development: BFS Finds extensive application in computing the minimal number of moves on a board game, maze or in a state-space problem.

 

BFS Algorithm (Step-by-Step Pseudocode)

Here is a simple pseudocode representation of BFS:

BFS(graph, start_node):
    create a queue and add start_node
    mark start_node as visited
    while queue is not empty:
        current = queue.pop(0)
        for each neighbor in graph[current]:
            if neighbor not visited:
                mark neighbor as visited
                queue.append(neighbor)

 

Implementing BFS in Python

Here is Python Python code of BFS with adjacency list representation of a graph:

from collections import deque

def bfs(graph, start):
    visited = set()             # Track visited nodes
    queue = deque([start])      # Initialize queue with the start node
    visited.add(start)
    
    while queue:
        node = queue.popleft()  # Remove the first element
        print(node, end=" ")    # Process the node (e.g., print it)
        
        for neighbor in graph[node]:
            if neighbor not in visited:
                visited.add(neighbor)
                queue.append(neighbor)

# Example graph (Adjacency List)
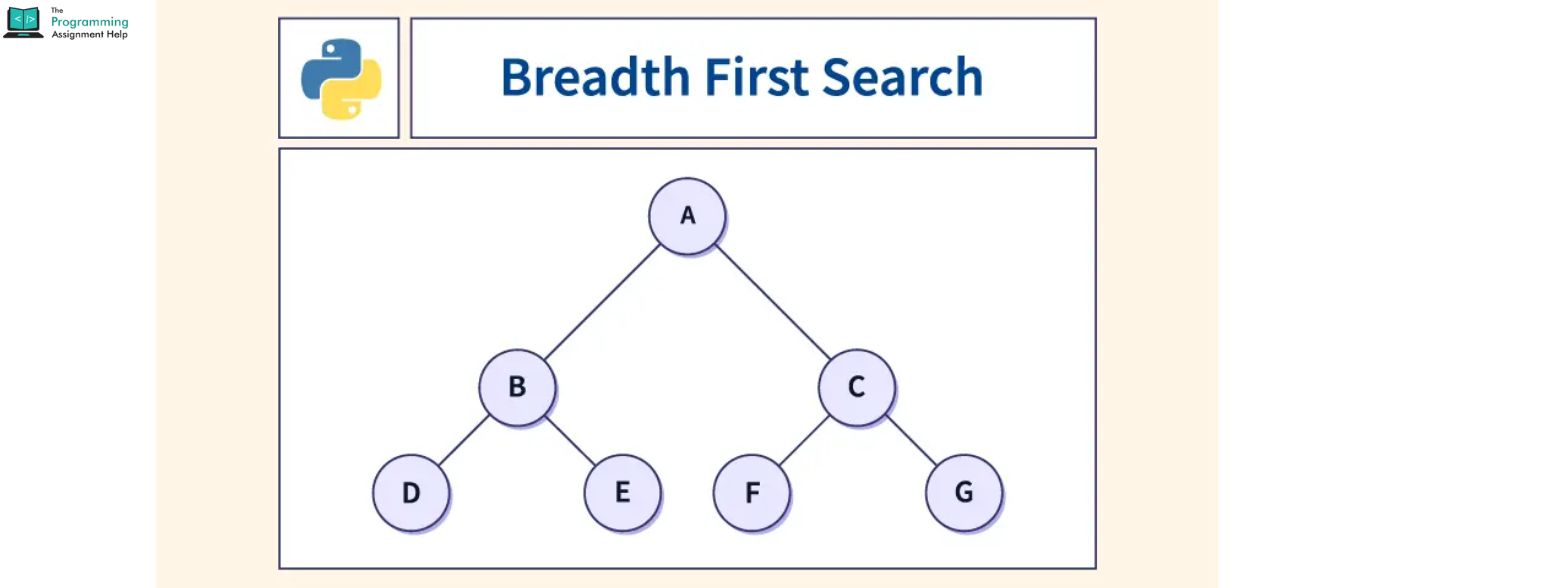
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

# Run BFS starting from node 'A'
bfs(graph, 'A')

Output:
mathematica
A B C D E F

 

Time and Space Complexity

• Time Complexity: O(V + E)

Here, V is the number of vertices, and E is the number of edges. BFS visits each node and edge once.

• Space Complexity: O(V)

Due to the queue and visited set, BFS needs space proportional to the number of vertices.

 

Common Mistakes in BFS Implementation

• Not marking nodes as visited early: It may cause nodes to be processed again and again, thus affecting efficiency.
• Using a list instead of deque for the queue: Python lists have O(n) pop(0) implementations, while deque comes up with O(1).
• Forgetting edge cases: Such as disconnected graphs or graphs with cycles.

 

Advanced Variations of BFS

• BFS for Shortest Path: With an additional parent dictionary, BFS can reconstruct the shortest path between two nodes.
• BFS on Grids: Used for maze solving or when you need to search for path in 2D matrix.
• Bidirectional BFS: Performs two BFS searches in parallel (one of the start and one of the goal) in order to accelerate pathfinding.

 

Need Help with BFS or Coding Projects?

If you find BFS implementation tricky or struggle with graph algorithms, our Coding Assignment Help and Coding Project Help services are here to guide you. We offer:

• Step-by-step explanations with working code.
• Error debugging and optimization.
• Custom BFS solutions for academic projects.

Our experts explain difficult concepts in an easy-to-follow manner whether you are an amateur or already dealing with advanced algorithms.